Intro To Recurrences (And DP)

What Are Recurrences?

Let's start with a simple problem: 

There are N students standing in a line. The first student gets 1 chocolate. The second student gets 2 chocolates. The third student however demands that he gets twice as many chocolates as the first student plus the number of chocolate that the second student got. Similarly, the fourth student said that he wanted twice the amount of chocolate that the second student got plus the amount the third student got. Thus, each student wants the amount that the previous student got plus twice the amount the student before that had got. We need to find the total number of chocolate that we are going to need to give to all the students. 

The obvious solution is to first give student1 1 chocolate, student2 2 chocolates, student3  2*1+2=4 chocolates, student4 = 2*2+4=8 chocolates and so on and then take the sum of all the chocolates that the students had got. Well, the key idea here was that if we know how many chocolates the (n-1)th and the (n-2)th student got, then we can calculate the number of chocolates for student n by the formula 2*(chocolates for (n-2)th student) + chocolates for the (n-1)th student. Pretty easy right?

This is primarily what we call a recurrence. Didn't get? Let me elaborate...

Function Form

Firstly, let's get into a more mathematical representation. 

Let F(x) denote the number of chocolate that the x'th student gets.

Get this very clear. This is JUST what the function denotes. We don't really know how it's calculated or anything. When we are given the value for F(x) the only thing that this means is that the Xth student got those many chocolates. We DO NOT care how it is calculated. That is a separate issue. 

So when we define something in terms of a function, there are generally two parts: what it means and how it is calculated. It is essential to distinguish between the two. Most of the times, we define a function to be something very simple. It's the calculation of the function that's troublesome. Nonetheless there should not be any confusion regarding what the function means with respect to how it is calculated.

That being said, let's see how F(x)  is calculated:

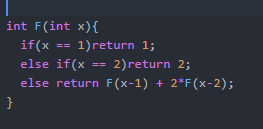
• F(1) = 1
• F(2) = 2
• F(x) = 2*F(x-2) + F(x-1)    

This is exactly what we were doing earlier. But now it's a bit easier to formulate and write. 

The above function that we got is what we call a recurrence or a recursively defined function. What it means? It just means that when u calculate F(x), you just need to know the values of

  F(x-1) and F(x-2)  and then we are done. Thus, when we want to know the value of the function for a certain x,  we need to know some of the previous values of the function. Thus it is defined ON itself, intuitively speaking. 

This might seem silly. After all, we were calculating the values just fine without all this recurrence. Turns out, there is some magic involved in this. Think like this: suppose we want to calculate the value of a certain function F(x) for some value of x. For that, if we know how the function is calculated, that is, on which of the earlier values of "states" of the function it depended on, we can magically assume that we know the answers to those previous values. Of course we will actually need to calculate them too, but there is a special advantage to thinking like this, which i will come to later. 

Another useful way in which we can define a recursive function or a recurrence is by saying that we are solving some smaller "subproblems" and then we are somehow combining the answers to all those subproblems to get the answer to our final problem. 

Recursive Function

Recursive functions are the computer's way of trying to replicate this. Let's see how this above function can be implemented in a computer:

Just as we defined our function!

This is why I said that we can assume that the previous values of F(x) were already somehow magically calculated as if we just assume that they were calculated, without thinking about how, we can easily get our final answer. Note however, that we are INDEED  calculating the previous values of the function: after all in the last line we ARE calling the same function with a smaller parameter, but in this way, its easier to just worry about combining the "smaller subproblems" that on actually computing these subproblems.

So to give some intuition to this code. Here, when we get a value of x as input, this calls ITSELF but two smaller values as parameter. Thus to calculate this "problem" that we were given, we are now trying to solve two other "subproblems" so that we can then combine the results and return our final answer. Note that we are not breaking our given problem every time. In case it's x=1 or x=2, we already know the answer. These are what we call as "base case" of this recursive function. Note that due to the presence of these base cases, we do not infinitely recurse: our recursion is "stopped" at some point by these bases cases, where we can return these precomputed value. 

Other examples

Fibonacci 

This is defined(rather calculated as Fibonacci numbers do not have any special meaning as such) as follows:

• F(0) = 0
• F(1) = 1
• F(n) = F(n-1) + F(n-2)

Again, the code to calculate this is very simple:

Once again, the code is exactly similar to what we had in the function's calculation. 

Again, we can magically assume that we know the values of its previous values and thus we can simple combine these values to get our answer. 

Factorial

The factorial funtion is calculated as follows:

• F(0) = 1
• F(n) = F(n-1) * n

The code? Well .. you can guess it :p

Going Further

What we have discussed till now are very basic recurrences. We can also have more complex functions which are defined by more that one parameters and whose calculation are more complex that what we have seen here. For example, suppose we are given a grid of N columns and M rows.

We want to go from the bottom left corner(0,0) to the top right corner(M,N). Also it is given that we can move only one row up or one column right at a time. 

Of course we can derive a formula for this easily. But how to represent it as a recursive function? 

Well, let F(col, row) denote the number of ways we can get to the cell with coordianates (col,row) from cell (0,0). Calculation is as follows:

• F(0,0) = 1
• F(-1,x) = F(x,-1) = 0 for any value of x (obviously, we cannot go outside the grid)
• F(col,row) = F(col-1,row) + F(col,row-1)

This basically says that the last step we took to reach to this cell could either have been a up-step or a right-step. Thus we could have come to this cell only if we were at cell (col-1,row) or (row-1,col). Thus the total number of ways we could have got here is number of ways we could have gone to (col-1,row) plus the number of ways we could have gone to cell (col,row-1).

Again the code will be very similar to the actual function calculation. Final answer is just the value F(M,N).