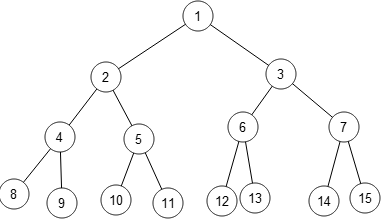
Intro To Recurrences (And DP)
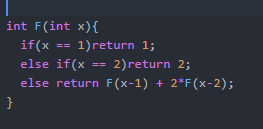
What Are Recurrences? Let's start with a simple problem: There are N students standing in a line. The first student gets 1 chocolate. The second student gets 2 chocolates. The third student however demands that he gets twice as many chocolates as the first student plus the number of chocolate that the second student got. Similarly, the fourth student said that he wanted twice the amount of chocolate that the second student got plus the amount the third student got. Thus, each student wants the amount that the previous student got plus twice the amount the student before that had got. We need to find the total number of chocolate that we are going to need to give to all the students. The obvious solution is to first give student1 1 chocolate, student2 2 chocolates, student3 2*1+2=4 chocolates, student4 = 2*2+4=8 chocolates and so on and then take the sum of all the chocolates that the students had got. Well, the key idea here was that if we know how many chocolates th