Trees

Trees

Trees are a special form of undirected graphs. It is basically a graph that is only 1 connected component and that has no cycles in it.

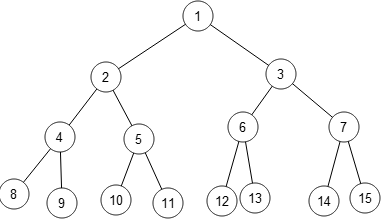
We generally draw a tree in a "reverse-tree" way --- starting from a single node and then branching out as it goes lower and lower. The main properties of a tree? As mentioned above, it has no cycles. and each node has exactly 1,what we call , parent, and multiple children. Here, for example, 3 has parent 1 and children 6 and 7. 4 has 2 as its parent and 8 and 9 as its children. A node can have any number of children, but exactly 1 parent. EXCEPT the "root" node. Here for example, node 1 is the root node.

The root node is very important. It is used in several calculations that are performed in a tree.  It is also the starting point for a BFS or a DFS in a tree. However, note how BFS and DFS are so much simpler in a tree rather than in a general graph. Here, when we do a DFS, we only go downwards and never upwards if we just keep track of its parent. So the code becomes like this: 

Note that in a tree, between each node, there is only 1 path. However in a graph, between 2 nodes, there can be multiple paths that connect them. Here, we consider two paths diffrent if there is atleast one node that one path visits that the other path dosn't.

Also note that in a tree, the number of Edges is exactly N-1 if N is the number of nodes in the tree. Turns out, the opposite is also true : if in a graph we somehow find that the number of edges is exactly N-1 then that means that the graph is a tree.

What about shortest paths in a tree? Well, since there is only 1 unique path in a tree, shortest path finding is easy. Suppose we start at node u and want to find lenght of path (u,v). Just start a dfs from node u and the answer is the distance when the dfs enters the node v.

Pseudocode is something like this: 

Thus, since complexity of each DFS is O(N) , each time we want to find the distance between two nodes, we can do so in linear time.

LCA 

Lca or the lowest common ancestor is just node with the maximum depth that occurs in both the path (root,u) and (root,v). Let's call this LCA(u,v). In the first diagram, LCA(6,7) is 3, LCA(9,10) is 2 and LCA(8,12) is 1. It can be also said to be the first time when, while going from u to root and from v to root we access a common vertex.

Now we can compute path between (u,v) in another way. 

(u,v) = (u,  LCA(u,v)) + (LCA(u,v) , v)

But how does this help? Whatever calculations we still might have to do, we will again need a DFS to compute for all these paths. Well turns out that in many cases it is not so.

The RHS of our previous eqn can be further simplified into this: 

(u,root) + (root,v) - 2*(root,LCA(u,v))  = (u,v)

Magic, right B) ? 

How does this help? Well, for one thing, all distances are now in terms of the root. So if we just do a DFS from root in the starting then we can compute the distance to all nodes. Then, however many queries we get, we just have to calculate the LCA and bingo! we then just add and subtract some values in constant time as the distances from root have already been calculated.

Turns out, LCA calculation can also be done in O(logn) time, which thus becomes the dominant factor. Hence, we have reduced computation of distance between two nodes from O(N) time to O(logn) time per query. With some linearithmic precomputation of course.

To notch it up a bit, any function that is commutative can be computed in this way, PROVIDED that the edge weights are not updated in between the queries.

To learn how to calculate the LCA, here is a tutorial. However, this is fairly complex.