Coding Start Up!

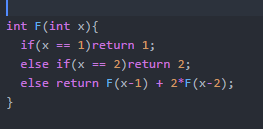
What Are Recurrences? Let's start with a simple problem:  There are N students standing in a line. The first student gets 1 chocolate. The second student gets 2 chocolates. The third student however demands that he gets twice as many chocolates as the first student plus the number of chocolate that the second student got. Similarly, the fourth student said that he wanted twice the amount of chocolate that the second student got plus the amount the third student got. Thus, each student wants the amount that the previous student got plus twice the amount the student before that had got. We need to find the total number of chocolate that we are going to need to give to all the students.  The obvious solution is to first give student1 1 chocolate, student2 2 chocolates, student3  2*1+2=4 chocolates, student4 = 2*2+4=8 chocolates and so on and then take the sum of all the chocolates that the students had got. Well, the key idea here was that if we know how many cho...

Spanning Trees in a Graph We are given a graph with say N vertices and M edges. We call a subset of these edges a spanning tree  of the graph so that if we keep only these edges, the graph still remains connected and so that the residual graph is a tree. This can also be thought of as specifying discreetly that we have to select exactly N-1 edges out of the total M that we are given. Some points that should be specified here is that there can be a lot of different number of spanning trees of a graph. Also, ALL the nodes need to be connected by the set of edges that we had selected in our spanning tree. Moreover, it doesn't really depend on whether we have weighted edges or unweighted edges, though we will shortly be looking at different types of spanning trees, some of which do take advantage of edge weights.  Finding Spanning Trees To find any random spanning tree of a graph a simple DFS will obviously suffice. Assuming the graph is connected,...

DISCLAIMER: I will not  be going over centroid tree. Just the decomposition technique as its far more useful than the actual centroid tree. Usefulness Before I describe the technique, it's better if i go over the usefulness of this technique first. Suppose we have been given a problem where we have to find the sum of F that is commutative that we have to compute over all possible paths in out tree. Oh and yes.. THIS TECHNIQUE IS ONLY FOR TREES . For now, let F be sum of edgeweights. Note that this could be done using other techniques too, and even faster than centroid decomposition, but this will serve as a nice example for the basics. We will approach harder problems later. Main Idea So the idea here is, it would be very nice if we could root the tree at some point, and then calculate this function for all paths passing through the root. This would have been done easily with a DFS. The problem is, we will then need to root the tree at various points, and calculate ...

Euler Tour        We mostly divide our problems into mostly two types: Array problems and Tree/Graph problems.  But what if we can convert some specific type of tree problems into actually array problems?  Problem: We are given a Tree. We have to perform two types of operations:   Query: Find the sum of weights of all nodes in the subtree of the given query node. Update: Set the weight of a given node to X. Obvious Solution? For each update just make the corresponding weight of the given node to X. For Queries, traverse the whole subtree and find the sum. This has a worst case of O(N*Q). However we will come up with a O(nlogn) solution to this same problem by the end of this post. Start Time/End Time When we do a DFS, suppose we keep a global variable called time.Whenever we visit a new node, we are doing something new and thus we "increase" the time. This can be thought of as a time variable that we are manuall...

Trees Trees are a special form of undirected graphs. It is basically a graph that is only 1 connected component and that has no cycles in it. We generally draw a tree in a "reverse-tree" way --- starting from a single node and then branching out as it goes lower and lower. The main properties of a tree? As mentioned above, it has no cycles. and each node has exactly 1,what we call , parent, and multiple children. Here, for example, 3 has parent 1 and children 6 and 7. 4 has 2 as its parent and 8 and 9 as its children. A node can have any number of children, but exactly 1 parent. EXCEPT the "root" node. Here for example, node 1 is the root node. The root node is very important. It is used in several  calculations that are performed in a tree.  It is also the starting point for a BFS or a DFS in a tree. However, note how BFS and DFS are so much simpler in a tree rather than in a general graph. Here, when we do a DFS, we only go downwards and never ...

Types Of Graphs We generally encounter the following types of graph in a problem. Each of them has some special properties which are often useful. Trees - This is by FAR the most common thing we shall encounter. Some don't even consider problems based on it as graph problems, still I will add this here for sake of completeness. Directed Acyclic Graphs (DAGs) - This is also a commonly recurring type of graph with lots of nice properties. For example, since cycles (acyclic .. duhh) do not exist, we are able to easily calculate DP on it. Later, we will show how ALL DP problems are just DAGs.  Planar graphs - These are quite rare but do appear in problems nonetheless. Special properties includes the application of euler's theorem and consideration of its dual graph. The vanilla version - This is our plain old graph, either directed or undirected. There are no special properties for this graph. Implicit graphs - sometimes the problem statement may not directly look like...

Some More Notations I will start with some notation first. Though this will be very short. First, when talking about nodes, we just refer to them using numbers. Or using alphabets. When using examples, it's rare that we will ever consider more than 26 nodes ( normally less than 10). Second, when talking about edges, we refer to them as e = (u,v) which means that edge e connects node u to node v. Somehow we generally use characters like u,v,w to refer to nodes. Just a preference.  When referring to undirected graphs, we use lines to represent them. Directed versions generally have arrows to point form where the edge is starting and where it is ending. When referring to a graph, we use the notation G = (V,E) which means that Graph G has vertices belonging to the set V and edges belonging to the set E. Note that the edges in E has its endpoints as vertices in V. (think about it... if it were not so.. then that edge would not have much meaning). Another thing th...

Introduction Let's start with a description: "There are several cities in a country. Suppose N cities for now. Suppose there are M roads,each of which connects some 2 pair of cities. " A very common description found in a huge number of problems. But what is this actually? How to usefully use this information, which seems to be a very obvious thing in out real life? Well, lets model this in terms of what we call "Graph theory". Not that it has much connection to the canonical definition of a graph that we generally encounter in our schools. The two main, MAIN, concepts in graph theory is a "node" and an "edge". Nodes can be said to be a "place" and edge can be thought of as a way to get from one "place" to another "place". In the above problem, we basically have N nodes, and M edges. Each edge just connects two nodes. Here the nodes are depicted by circles, and the edges are denoted by the s...